16.
Ako su data dva kruga sa istim centrima, upisati u veći krug jednakostrani mnogougao, sa parnim brojem strana koji ne dodiruju manji krug.
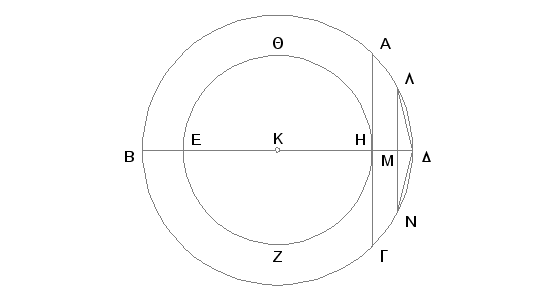
Neka su data dva kruga ABGD i EZHQ sa istim centrom K. Treba u veći krug ABGD upisati jednakostrani mnogougao sa parnim brojem strana koji ne dodiruje krug EZHQ.
Povucimo kroz centar K pravu BKD, a kroz tačku prave BD povucimo, pod pravim uglom, pravu HA i produžimo je do G. Prava AG je, prema tome, tangenta kruga EZHQ [III.16, Posledica]. Prepolovimo luk BAD i njegovu polovinu ponovo prepolovimo; postupajući tako stalno, dobićemo luk manji od AD [X.1]. Neka je to postignuto i neka to bude LD; i iz tačke L spustimo na BD normalu LM i produžimo do N, i povucimo LD i DN; tada je LD jednako DN [III.3, I.4]. Pošto je LN paralelna sa AG, a AG tangenta kruga EZHQ prava LN neće dodirivati krug EZHQ. Utoliko pre duži LD, DN neće dodirivati krug EZHQ. Prema tome, ako u krugu ABGD počnemo crtati prave jednake LD, biće u krug ABGD upisan jednakostran mnogougao, sa parnim brojem strana, koji ne dodiruje manji krug EZHQ. A to je trebalo izvesti.