18.
Razmera jedne lopte prema drugoj je triput viša od razmere njihovih prečnika.
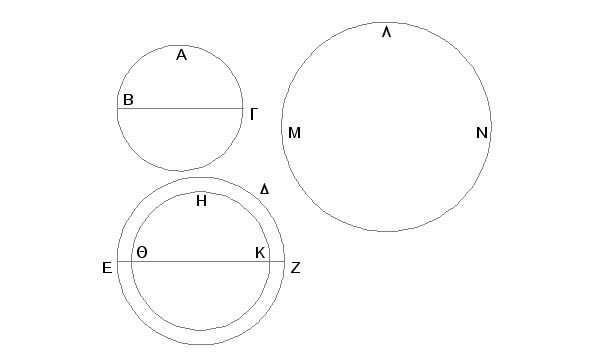
Zamislimo lopte ABG i DEZ; neka su im prečnici BG i EZ. Tvrdim da je razmera lopte ABG prema lopti DEZ triput viša od razmere BG prema EZ.
Zaista, ako razmera lopte ABG prema lopti DEZ nije triput viša od razmere BG prema EZ, biće razmera lopte ABG triput viša od razmere BG prema EZ ili prema lopti manjoj od lopte DEZ ili prema većoj. Neka bude, prvo, prema manjoj, naime prema HQK. Zamislimo lopte DEZ i HQK oko istog centra. Upišimo u veću loptu DEZ poliedarsko telo telo koje ne dodiruje površinu manje lopte HQK [XII.17]. Upišimo i u loptu ABG poliedarsko telo slično poliedarskom telu upisanom u loptu DEZ. Tada je razmera poliedarskog tela upisanog u loptu ABG prema poliedarskom telu upisanom u loptu DEZ triput viša od razmere GB prema EZ [XII.17, Posledica]. Ali i razmera lopte ABG prema lopti HQK je triput viša od razmere BG prema EZ. Prema tome se lopta ABG odnosi prema lopti HQK kao poliedarsko telo upisano u loptu ABG prema poliedarskom telu upisanom u loptu DEZ. Posle promene reda, lopta ABG se odnosi prema njenom poliedru kao lopta HQK prema poliedarskom telu upisanom u loptu DEZ [V.16]. I lopta ABG je veća od njenog poliedra. Veća je prema tome i lopta HQK od poliedra u lopti DEZ. Ali je i manja, jer je ona njime obuhvaćena. Znači, lopta ABG nije prema manjoj lopti DEZ u razmeri triput višoj od razmere prečnika BG prema EZ. Slično se dokazuje da je lopta DEZ prema lopti manjoj od lopte ABG u razmeri triput višoj od razmere EZ prema BG.
Tvrdim da lopta ABG nije ni prema lopti većoj od lopte DEZ u triput višoj razmeri od razmere BG prema EZ.
Zaista, ako je moguće, neka bude prema većoj LMN. Znači, obrnuto: lopta LMN je prema lopti ABG u triput višoj razmeri od razmere prečnika EZ prema prečniku BG. Ali se lopta LMN odnosi prema lopti ABG kao lopta DEZ prema nekoj manjoj lopti od lopte ABG, pošto je lopta LMN, kako je ranije dokazano, veća od lopte DEZ [XI.2, Lema]. Na ovaj način lopta DEZ se odnosi prema lopti manjoj od lopte ABG u triput višoj razmeri od razmere EZ prema BG. A dokazano je da je to nemoguće. Prema tome lopta ABG nije prema lopti većoj od lopte DEZ u razmeri triput višoj od razmere BG prema EZ. A dokazano je da nije ni prema manjoj.
Na ovaj način lopta ABG je prema lopti DEZ u razmeri triput višoj od razmere BG prema EZ. A to je trebalo dokazati.