7.
Svaka prizma sa trouglom u osnovi može se podeliti na tri među sobom jednake piramide sa trouglovima u osnovama.
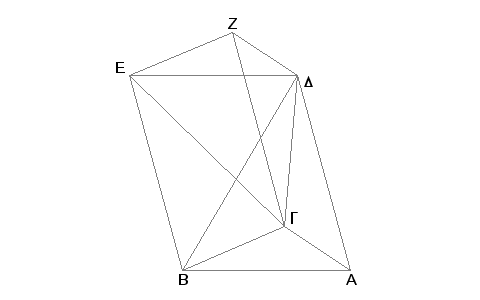
Neka je data prizma kojoj je trougao ABG u osnovi i naspramni trougao DEZ. Tvrdim da se prizma ABGDEZ može podeliti na tri među sobom jednake piramide sa trouglovima u osnovama.
Zaista, povucimo BD, EG i GD. Pošto je ABED paralelogram, a BD je njegova dijagonala, biće trougao ABD jednak trouglu EBD [I.34]. Prema tome je piramida kojoj je trougao ABD u osnovi i vrh u tački G jednaka piramidi kojoj je trougao DEB u osnovi i vrh u tački G [XII.5]. Ali piramida kojoj je osnova trougao DEB i vrh u tački G ista je kao i piramida kojoj je osnova trougao EBG i vrh u tački D, jer su one obuhvaćene istim ravnima. I prema tome je piramida kojoj je osnova trougao ABD i vrh u tački G jednaka piramidi kojoj je osnova trougao EBG i vrh u tački D. Dalje, pošto je ZGBE paralelogram, a GE njegova dijagonala, trougao GEZ jednak je trouglu GBE [I.34]. I na taj način je piramida kojoj je osnova trougao BGE ivrh u tački D jednaka piramidi kojoj je osnova trougao EGZ i vrh u tački D [XII.5]. A dokazali smo da je piramida kojoj je osnova trougao BGE i vrh u tački D jednaka piramidi kojoj je osnova trougao ABD i vrh u tački G. Prema tome je piramida kojoj je osnova trougao GEZ i vrh u tački D jednaka piramidi kojoj je osnova trougao ABD i vrh u tački G. Na ovaj je način prizma ABGDEZ podeljena na tri među sobom jednake piramide sa trouglovima u osnovama.
I pošto je piramida kojoj je osnova trougao ABD i vrh u tački G ista sa piramidom kojoj je osnova trougao GAB i vrh u tački D, jer su one obuhvaćene istim ravnima, a, kako smo dokazali, piramida kojoj je osnova trougao ABD i vrh u tački G je jedna trećina prizme kojoj je osnova trougao ABG i naspramni trougao DEZ, biće, prema tome, piramida kojoj je osnova trougao ABG i vrh u tački D jedna trećina prizme kojoj je osnova isti trougao ABG i naspramni trougao DEZ.