8.
Razmera sličnih piramida kojima su osnove trouglovi triput je viša od razmere homolognih ivica.
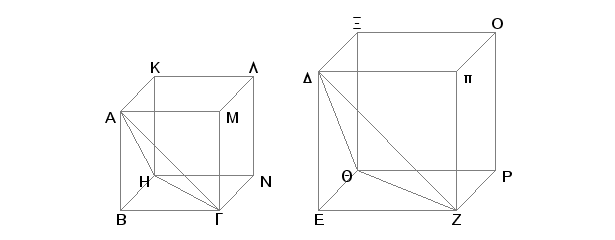
Neka su date slične i u sličnom položaju piramide kojima su osnove trouglovi ABG i DEZ i vrhovi u tačkama H i Q. Tvrdim da je razmera piramide ABGH prema piramidi DEZQ triput viša od razmere BG prema EZ.
Zaista, dopunimo paralelepipede BHML i EQpO. Pošto je piramida ABGH slična piramidi DEZQ, biće ugao ABG jednak uglu DEZ, ugao HBG uglu QEZ i ugao ABH uglu DEQ, i AB prema DE kao BG prema EZ i kao BH prema EQ. A kako je AB prema DE kao BG prema EZ, a to su proporcionalni kraci jednakih uglova, biće paralelogram BH sličan paralelogramu Ep. Iz istih razloga je i paralelogram BN sličan paralelogramu EP, BK - EX. Na taj način su tri paralelograma BM, BK, BN slična trima paralelogramima Ep, EX, EP. No tri paralelograma BM, BK, BN su jednaka i slična trima naspramnim paralelogramima, a isto tako su i tri paralelograma Ep, EX, EP jednaka i slična svojim naspramnim [XI.24]. Na taj način su tela BHML i EQpO obuhvaćena sličnim ravnim površinama u istom broju. Prema tome je telo BHML slično telu EQpO. No razmera sličnih paralelepipeda je triput viša od razmere homolognih ivica [XI.33]. Na ovaj način je telo BHML prema telu EQpO u triput višoj razmeri od razmere homologne ivice BG prema homolognoj ivici EZ. Ali telo BHML je prema telu EQpO prema piramidi DEZQ, jer je piramida šesti deo paralelepipeda, čija je polovina, kao prizma [XI.28], jednaka utrostručenoj piramidi [XII.7]. I na taj način je razmera piramide ABGH prema piramidi DEZQ triput viša od razmere ivice BG prema ivici EZ. A to je trebalo dokazati.