10.

Svaka kupa (konus) je trećina valjka (cilindra), ako imaju istu osnovu i jednake visine.

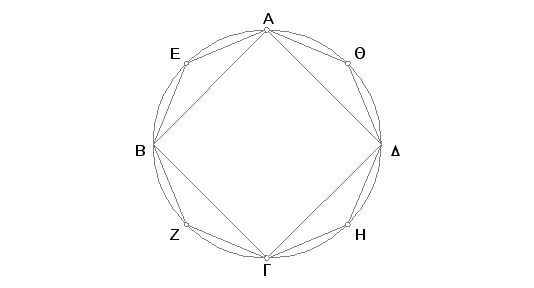
Neka kupa i valjak imaju isti krug ABGD za osnovu i jednake visine. Tvrdim da je kupa trećina valjka, tj. da je valjak triput veći od kupe.
Zaista, ako valjak nije triput veći od kupe, on će biti veći ili više no triputa ili manje no triputa. Neka prvo bude veći više no triputa. Upišimo u krug ABGD kvadrat ABGD [IV.6]. Taj kvadrat je veći od polovine kruga ABGD. Konstruišimo nad kvadratom ABGD prizmu sa visinom jednakom visini valjka. Konstruisana prizma je veća od polovine valjka, jer, ako oko kruga ABGD opišemo kvadrat [IV.7], upisani kvadrat je polovina opisanog, a tela konstruisana nad njima su prizme jednakih visina. A kako su prizme jednakih visina u razmeri njihovih osnova [XI.32], biće prizma konstruisana nad kvadratom ABGD jednaka polovini prizme nad kvadratom opisanim oko kruga ABGD [XI.28, XII.6, XII.7, Posledica]. A kako je valjak manji od prizme konstruisane nad kvadratom opisanim oko kruga ABGD, biće prizma konstruisana nad kvadratom ABGD sa visinom jednakom visini valjka veće od polovine valjka. Prepolovimo kružne lukove AB, BG, GD, DA tačkama E, Z, H, Q i povucimo AE, EB, BZ, ZG, GH, HD, DQ, QA. Tada je svaki od trouglova AEB, BZG, GHD, DQA veći od polovine otsečka kruga ABGD, kako smo ranije dokazali [XII.2]. Konstruišimo nad svakim od trouglova AEB, BZG, GHD, DQA prizmu koja ima visinu jednaku visini valjka. Tada je i svaka od konstruisanih prizama veća od polovine otsečka valjka, jer, ako kroz tačke E, Z, H, Q povučemo prave paralelne sa AB, BG, GD, DA dopunimo paralelograme na AB, BG, GD, DA i nad njima konstruišemo paralelepipede sa visinama jednakim visini valjka, polovina svakog je prizma konstruisana nad trouglovima AEB, BZG, GHD, DQA. I otsečci valjka su manji od konstruisanih paralelepipeda. Na taj način su prizme konstruisane nad trouglovima AEB, BZG, GHD, DQA veće od polovine otsečaka. Ako prepolovimo preostale kružne lukove, povučemo prave i konstruišemo nad svakim trouglom prizmu sa visinom valjka, onda, postupajući tako neprekidno, dobićemo na kraju takve otsečke valjka čiji će zbir biti manji od razlike valjka i utrostručene kupe [X.1]. Neka je to postignuto sa otsečcima AE, EB, BZ, ZG, GH, HD, DQ, QA. tada je preostala prizma, sa osnovom mnogouglom AEBZGHDQ i visinom valjka, veća od utrostručene kupe. No prizma kojoj je mnogougao AEBZGHDQ u osnovi i visina jednaka visini valjka jednaka je trostrukoj piramidi kojoj je mnogougao AEBZGHDQ osnova i vrh u vrhu kupe [XII.7, Posledica]. Prema tome je piramida kojoj je mnogougao AEBZGHDQ osnova i vrh u vrhu kupe veća od kupe sa krugom ABGD u osnovi, ali je ona i manja, jer je ona obuhvaćena kupom. A to je nemoguće. Prema tome valjak neće biti od utrostručene kupe.
Tvrdim da valjak neće biti ni manji od utrostručene kupe.
Zaista, ako je moguće, neka valjak bude manji od utrostručene kupe; znači, obrnuto, kupa je veća od trećine valjka. Upišimo u krug ABGD kvadrat ABGD. Tada je kvadrat ABGD veći od polovine kruga ABGD. Konstruišimo nad kvadratom AGBD piramidu sa vrhom u vrhu kupe. Konstruisana piramida je veća od polovine kupe, jer, kako smo već dokazali, ako opišemo oko kruga kvadrat, kvadrat ABGD biće jednak polovini kvadrata opisanog oko kruga. I ako na kvadratima konstruišemo paralelepipede, koji se zovu i prizme, sa visinama jednakim visini kupe, biće prizma konstruisana nad kvadratom ABGD polovina prizme konstruisana nad kvadratom opisanim oko kruga, jer su one u razmeri jedna prema drugoj kao osnove [XI.32]. A u istoj su razmeri i njihove trećine. Prema tome je piramida kojoj je kvadrat ABGD u osnovi polovina piramide konstruisane nad kvadratom opisanim oko kruga. A piramida konstruisana nad kvadratom opisanim oko kruga je veća od kupe, jer ona kupu obuhvata. Prema tome je piramida kojoj je kvadrat ABGD u osnovi i vrh u vrhu kupe veća od polovine kupe. prepolovimo kružne lukove AB, BG, GD, DA tačkama E, Z, H, Q i povucimo AE, EB, BZ, ZG, GH, HD, DQ, QA; tada je svaki od trouglova AEB, BZG, GHD, DQA veći od polovine odgovarajućeg otsečka kruga. Sad konstruišemo nad svakim od trouglova AEB, BZG, GHD, DQA piramidu sa istim vrhom kao i kupa. Svaka od konstruisanih piramida biće, na osnovu izvedenih rasuđivanja, veća od polovine odgovarajućeg otsečka kupe. Ako prepolovimo preostale kružne lukove, povučemo prave i konstruišemo nad svakim od trouglova piramidu sa vrhom u vrhu kupe, onda ćemo, tako postupajući neprestano, dobiti na kraju takve otsečke kupe, čiji će zbir biti manji od razlike kupe i trećeg dela valjka [X.1]. Neka je to postignuto sa otsečcima AE, EB, BZ, ZG, GH, HD, DQ, QA. Tada je preostala piramida kojoj je mnogougao AEBZGHDQ u osnovi i vrh u vrhu kupe, veća od trećine valjka. Ali je piramida kojoj je mnogougao AEBZGHDQ osnova i vrh u vrhu kupe trećine prizme kojoj je mnogougao AEBZGHDQ u osnovi i visina jednaka visini valjka. Prema tome je prizma kojoj je mnogougao AEBZGHDQ u osnovi i visina jednaka visini valjka veća od valjka sa krugom ABGD u osnovi. Ali je ona i manja, jer je valjak obuhvata. A to je nemoguće. Na ovaj način valjak neće biti manji od utrostručene kupe. A dokazano je da neće biti ni veći od utrostručene kupe. Prema tome je valjak utrostručena kupa, dakle kupa je trećina valjka.
Na ovaj način je svaka kupa trećina valjka, ako imaju istu osnovu i jednake visine. A to je trebalo dokazati.