11.

Kupe i valjci sa istom visinom odnose se jedno prema drugom, posebice, kao osnove.

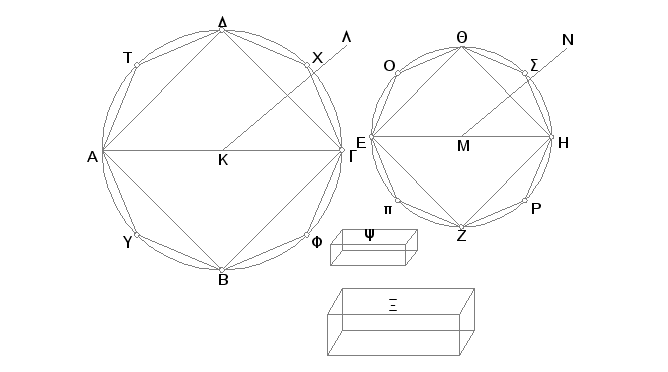
Neka su date kupe i valjci iste visine, njihove osnove su krugovi ABGD i EZHQ, ose - KL, MN, prečnici osnova AG i EH. Tvrdim, da se krug ABGD odnosi prema krugu EZHQ kao kupa AL prema kupi EN.
Zaista, ako nije, neka je krug ABGD prema krugu EZHQ kao kupa AL prema kupi ili manjoj od kupe EN ili većoj. Neka, prvo, bude prema manjoj X i neka je telo Y jednako razlici između kupe EN i tela X. Prema tome je kupa EN jednaka zbiru tela X i Y. Upišimo u krug EZHQ kvadrat EZHQ. Prema tome je taj kvadrat je veći od polovine kruga. Konstruišimo nad kvadratom EZHQ piramidu sa visinom kupe. Na ovaj način konstruisana piramida je veća od polovine kupe, jer, ako oko kruga opišemo kvadrat i nad njim konstruišemo piramidu sa visinom kupe, biće upisana piramida polovina opisane, pošto su one u razmeri osnova [XII.6]. Prepolovimo kružne lukove EZ, ZH, HQ, QE tačkama O, p, P, S i povucimo prave QO, OE, Ep, pZ, ZP, PH, pS, SQ. Prema tome je svaki od trouglova QOE, EpZ, ZPH, HSQ veći od polovine odgovarajućeg kružnog otsečka. Konstruišimo nad svakim od trouglova QOE, EpZ, ZPH, HSQ piramidu sa visinom jednakom visini kupe. I tada je svaka od konstruisanih piramida veća od polovine odgovarajućeg otsečka kupe. Ako prepolovimo preostale kružne lukove, povučemo prave i konstruišemo nad svakim trouglom piramidu sa visinom jednakom visini kupe, dobićemo, tako postupajući neprekidno, otsečke kupe, čiji je zbir manji od tela Y [X.1]. Neka je to postignuto sa QOE, EpZ, ZPH, HSQ. Prema tome je preostala piramida, kojoj je mnogougao QOEpZPHS osnova, visina jednaka visini kupe, veća od tela X. Upišimo i u krug ABGD mnogougao DTAUBFGX, sličan i u sličnom položaju sa mnogouglom QOEpZPHS, i konstruišimo nad njim piramidu sa visinom kupe AL. Pošto je sad kvadrat na AG prema kvadratu na EH kao mnogougao DTAUPFGX prema mnogouglu QOEpZPHS [XII.1], a kvadrat na AG je prema kvadratu na EH kao krug ABGD prema krugu EZHD [XII.2], biće krug ABGD prema krugu EZHQ kao mnogougao DTAUBFGX prema mnogouglu QOEpZPHS. Ali krug ABGD je prema krugu EZHD kao kupa AL prema telu X, a mnogougao DTAUBFGX prema mnogouglu QOEpZPHS kao piramida kojoj je mnogougao DTAUBFGX osnova i vrh u tački L prema piramidi kojoj je mnogougao QOEpZPHS osnova i vrh u tački N [XII.6]. I na taj način je kupa AL prema telu X kao piramida kojoj je mnogougao DTAUBFGX osnova i vrh u tački L prema piramidi kojoj je mnogougao QOEpZPHS osnova i vrh u tački N [V.11]. Na taj način, posle posle promene reda, kupa AL se odnosi prema piramidi u njoj kao telo X prema piramidi u kupi EN [V.16]. No kupa AL je veća od piramide u njoj. Pa prema tome je telo X veće od piramide u kupi EN. A ono je manje. A to je besmisleno. I tako se krug ABGD ne odnosi prema krugu EZHQ kao kupa AL prema telu manjem od kupe EN. Slično se dokazuje da se ni krug EZHQ ne odnosi prema krugu ABGD kao kupa EN prema telu manjem od kupe AL.
Tvrdim da se ni krug ABGD neće odnositi prema krugu EZHQ kao kupa AL prema telu većem od kupe EN.
Zaista, ako je moguće, neka bude prema većem telu X. Znači obrnuto: krug EZHQ je prema krugu ABGD kao telo X prema kupi AL. No telo X je prema kupi AL kao kupa EN prema telu manjem od kupe AL. I prema tome je krug EZHQ prema krugu ABGD kao kupa EN prema telu manjem od kupe AL. A ovo je, kako smo dokazali, nemoguće. Na taj način ne odnosi se krug ABGD prema krugu EZHQ kao kupa AL prema telu većem od kupe EN. A dokazano je da se ne odnosi ni prema manjem. Prema tome je krug ABGD prema krugu EZHQ kao kupa AL prema kupi EN.
No kupa je prema kupi kao valjak prema valjku, jer je svako triput veći od svakog [XII.10]. I prema tome se krug ABGD pdnosi prema krugu EZHQ kao i valjci konstruisani nad njima, sa jednakim visinama (sa kupama).
Na ovaj način, kupe i valjci sa istom visinom odnose se jedno prema drugom, posebice, kao osnove. A to je trebalo dokazati.