12.

Slične kupe među sobom i slični valjci među sobom su u razmeri triput višoj od razmere prečnika njihovih osnova.

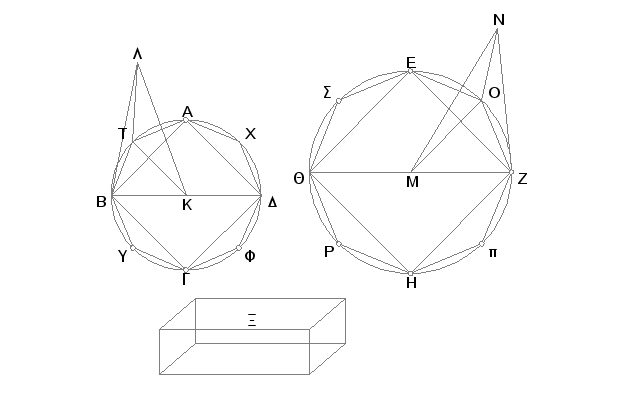
Neka su date slične kupe i slični valjci čije su osnove krugovi ABGD i EZHQ, prečnici BD i ZQ, a ose kupa i valjaka KL i MN. Tvrdim da je kupa kojoj je osnova krug ABGD i vrh u tački L prema kupi kojoj je osnova krug EZHQ i vrh u tački N u razmeri triput višoj od razmere BD prema ZQ.
Zaista, ako kupa ABGDL nije prema kupi EZHQN u razmeri triput višoj od razmere BD prema ZQ, biće onda kupa ABGDL u razmeri triput višoj ili prema telu manjem od kupe EZHQN ili prema većem telu. Neka, prvo, bude prema manjem telu X. Upišimo u krug EZHQ kvadrat EZHQ [IV.6]. Tada je kvadrat EZHQ veći od polovine kruga EZHQ. I konstruišimo nad kvadratom EZHQ piramidu sa vrhom u vhu kupe. Konstruisana piramida je veća od polovine kupe. Prepolovimo kružne lukove EZ, ZH, HQ, QE tačkama O, p, P, S i povucimo prave EO, OZ, Zp, pH, HP, PQ, QS, SE. Svaki od trouglova EOZ, ZpH, HPQ, QSE je manji od polovine odgovarajućeg otsečka kruga. Sad konstruišimo nad svakim od trouglova EOZ, ZpH, HPQ, QSE piramidu sa vrhom u vrhu kupe. I svaka od konstruisanih piramida je veća od polovine odgovarajućeg otsečka kupe. Ako prepolovimo preostale kružne lukove, povučemo prave i konstruišemo nad svakim trouglom piramidu sa vrhom u vrhu kupe, onda ćemo, postupajući tako neprestano, dobiti na kraju otsečke kupe čiji će zbir biti manji od razlike kupe EZHQN i tela X [X.1]. Neka je to postignuto sa EO, OZ, Zp, pH, HP, PQ, QS, SE. Tada je preostala piramida kojoj je mnogougao EOZpHPQS u osnovi i vrh u tački N veća od tela X. Upišimo i u krug ABGD mnogougao ATBUGFDX sličan i u sličnom položaju sa mnogouglom EOZpHPQS, i konstruišimo nad mnogouglom ATBUGFDX piramidu sa vrhom u vrhu kupe, i neka je LBT jedan od trouglova bočne površine piramide kojoj je mnogougao ATBUGFDX u osnovi i vrh u tački L, ANZO jedan od trouglova bočne površine piramide kojoj je mnogougao EOZpHPQS u osnovi i vrh u tački N, i povucimo KT i MO. Pošto je kupa ABGDL slična kupi EZHQN, biće BD prema ZQ kao osa KL prema osi MN [XI, Def. 24]. I BD je prema ZQ kao BK prema ZM. I prema tome je BK prema ZM kao KL prema MN [V.16]. No kraci jednakih uglova su proporcionalni, prema tome je trougao BKL sličan trouglu ZMN [VI.6]. Zatim, pošto je BK prema KT kao ZM prema MO i to su kraci jednakih uglova BKT, ZMO, jer je ugao BKT isti deo od četiri prava ugla kod centra K, koji je i ugao ZMO od četiri prava ugla kog centra M. Pošto su sad kod jednakih uglova kraci proporcionalni, biće trougao BKT sličan trouglu ZMO [VI.6]. Zatim, pošto je dokazano, da je BK prema KL kao ZM prema MN, BK jednako KT, a ZM - OM, onda je TK prema KL kao OM prema MN. I to je kod jednakih uglova TKL i OMN, jer su oni pravi. Kako su strane proporcionalne, trougao LKT je sličan trouglu NMO [VI.6]. I pošto je, zbog sličnosti trouglova BKT i ZMO, KB prema BT kao MZ prema ZO. Zatim, pošto je, zbog sličnosti trouglova LTK, NOM, LT prema TK kao NO prema OM i, zbog sličnosti trouglova TKB i OMZ, KT je prema TB kao MO prema OZ, biće, zbog jednakoudaljenosti, LT prema TB kao NO prema OZ [V.22]. A dokazali smo da je i TB prema BL kao OZ prema ZN. Na taj način, zbog jednakoudaljenosti, TL je prema LB kao ON prema NZ [V.22]. Prema tome su strane trouglova LTB i NOZ proporcionalne. Znači trouglovi LTB i NOZ imaju jednake uglove [VI.5], te su prema tome slični [VI, Def. 1]. Na taj način je piramida kojoj je trougao BKT u osnovi i vrh tački L slična piramidi kojoj je trougao ZMO u osnovi i vrh u tački N, jer su one obuhvaćene sličnim ravnima u istom broju [XI, Def. 9]. Ali je razmera sličnih piramida koje imaju trouglove u osnovama triput viša od razmere homolognih ivica [XII.8]. Prema tome je razmera piramide BKTL prema piramidi ZMON triput viša od razmere BK prema ZM. Na sličan način, ako povučemo prave iz A, X, D, F, G, U ka K iz E, S, Q, P, H, p ka M i konstruišemo nad svim trouglovima piramide sa vrhovima u vrhu kupa, može se dokazati da je razmera svake od piramida prema svakoj piramidi u sličnom položaju viša od razmere ivice BK prema homolognoj ivici ZM, tj. razmere BD prema ZQ. I pošto je jedan prethodni prema jednom narednom kao zbir svh prethodnih prema zbiru svih narednih [V.12], biće piramida BKTL prema piramidi ZMON kao cela piramida kojoj je mnogougao ATBUGFDX u osnovi i vrh u tački L prema celoj piramidi kojoj je mnogougao EOZpHPQS u osnovi i vrh u tački N. Prema tome je razmera piramide kojoj je mnogougao ATBUGFDX u osnovi i vrh u tački L prema piramidi kojoj je mnogougao EOZpHPQS u osnovi i vrh u tački N triput viša od razmere BD prema ZQ. A pretpostavlja se da je i razmera kupe kojoj je krug ABGD u osnovi i vrh u tački L prema telu X triput viša od razmere BD prema ZQ. Na ovaj način je kupa kojoj je krug ABGD u osnovi i vrh u tački L prema telu X kao piramida kojoj je mnogougao ATBUGFDX osnovni i vrh u tački L prema piramidi kojoj je mnogougao EOZpHPQS u osnovi i vrh u N. Ili, posle promene reda, kupa kojoj je krug ABGD u osnovi i vrh u L se odnosi prema svojoj piramidi kojoj je mnogougao ATBUGFDX u osnovi i vrh u tački L kao telo X prema piramidi kojoj je mnogougao EOZpHPQS u osnovi i vrh u N [V.16]. Ali pomenuta kupa je veća od piramide, jer je obuhvata. Prema tome i telo X je veće od piramide kojoj je mnogougao EOZpHPQS u osnovi i vrh u N. No ono je i manje. A to je nemoguće. Na ovaj način kupa kojoj je krug ABGD u osnovi i vrhu L neće biti u razmeri prema nekom telu manjem od kupe kojoj je krug EZHQ u osnovi i vrh u N u triput višoj razmeri od razmere BD prema ZQ. Slično se dokazuje da i kupa EZHQN neće biti prema telu manjem od kupe ABGDL u razmeri triput višoj od razmere ZQ prema BD.
Tvrdim da kupa ABGDL neće biti ni prema telu većem od kupe EZHQN u razmeri triput višoj od razmere BD prema ZQ.
Zaista, ako je to moguće, neka bude prema većem telu X. Prema tome, obrnuto, telo X je prema kupi ABGDL u razmeri triput višoj od razmere ZQ prema BD. Telo X je prema kupi ABGDL kao kupa EZHQN prema telu manjem od kupe ABGDL. Dakle, kupa EZHQN je prema telu manjem od kupe ABGDL u razmeri triput višoj od razmere ZQ prema BD. A dokazano je da je to nemoguće. Prema tome kupa ABGDL prema telu većem od kupe EZHQN nije u razmeri triput višoj od razmere BD prema ZQ. A dokazano je da nije ni prema manjem telu. Na ovaj način kupa ABGDL je prema kupi EZHQN u razmeri triput višoj od razmere BD prema ZQ.
Ali kupa prema kupi je kao valjak prema valjku, jer je valjak triput veći od kupe sa istom osnovom i visinom [XII.10]. Prema tome je i valjak prema valjku u razmeri triput višoj od razmere BD prema ZQ.
Na ovaj način, slične kupe među sobom i slični valjci među sobom su u razmeri triput višoj od razmere prečnika njihovih osnova. A to je trebalo dokazati.